Introduction

Part 1 of these notes introduced the concepts underlying a 2D alpha shape utility. Part 2 discussed implementation details from the AlphaShape class. This section of the notes provides the derivation for the alpha circle calculations which are used extensively within the AlphaShape class.

The process of building an alpha shape from a Delaunay triangulation is based on determining which edges in the triangulation are to be included in the shape and which are external to its bounds (i.e. which edges are "exposed"). The choice of which edges are exposed is based on the alpha circle selection criterion

The alpha circle calculation

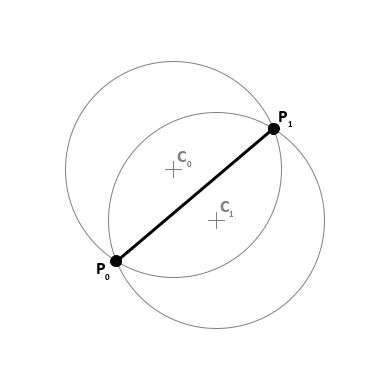
The key calculation needed to construct an alpha circle is to find the centers for two circles of radius r that intersect a line segment of length 2r or less. This calculation can be accomplished using basic algebra, though a software implementation needs to make a few adjustments to compensate for the limits of floating-point arithmetic. In particular, when processing geospatial data, we are often faced with coordinates that are separated by small distances but have a large magnitude. And, under some circumstances, calculations with large-magnitude values suffer a loss of precision when low-order digits drop out of addition or subtraction operations. So the calculation below uses a simple offsetting transformation to reduce the magnitude of the values the software needs to process in a numerical calculation.

Given a line segment with distinct endpoints and , we wish to find the coordinates for the centers of two alpha circles and .

Let

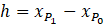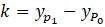This specification essentially transforms the endpoints of the segment to a new coordinate system in which they are defined as (0, 0) and (h, k). Because both endpoints are at distance r from the center (x, y) of an alpha circle, we can use the distance formula to obtain the relationships shown below in [1]. While these equations superficially resemble the standard equations for a circle, they are actually intended to allow us to find the centers of the circles. Those centers are found by solving the equations for x and y. As we would expect, the equations lead to two solutions, one for each circle.

Once we find the pair solutions for (x, y), we can transform the results back to the original coordinate system by adding back the offset for .

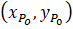[1]

Solving the two simultaneous equations in [1] for y as a function of x, we have

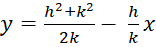[2]

assuming that k is not zero.

Let

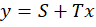[3]

with

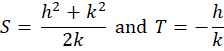Substituting [3] into [1], we have

and

[4]

Solving the quadratic equation [4] gives us two values for x corresponding to the centers of the two circles:

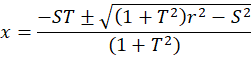Designating the values of x as x₀ and x₁, compute y₀ and y₁ using [2]. Then for each coordinate pair, we have circle centers

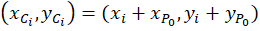Special cases exist when the line segment is of length 2r (the quadratic has a single solution), length greater than 2r (the quadratic has no solution), and the line segment is of zero length (the two endpoints are not distinct and an alternate, trivial solution applies).

In the equations above, we assume that the value for k is not zero and allow it to appear in the denominator for some of the equations. If k is zero, then the y coordinates of the line segment would be equal and there is a simpler calculation that we could use for the circle centers. But doing so would not address the floating-point arithmetic issues that would arise when k was non-zero but had a very small absolute value. To avoid putting near-zero values in the denominator, Tinfour uses an alternate derivation of the calculation for circle centers. When it puts h in the denominator rather than k by solving the simultaneous equations in [1] to get x as a function of y.

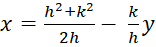[5]

This expression closely resembles expression [2] which gave us y as a function of x. The rest of the alpha-circle calculation follows in a manner similar to the steps above: solve the quadratic equation for y and compute the two values x₀ and x₁ from y₀ and y₁.

In Tinfour's AlphaCircle class, there are two blocks of code for computing the circle centers. One puts h in the denominator. The other puts k in the denominator. The logic selects which block to use based on which of the two variables has the largest absolute value. While there is some redundancy in the code, this approach neatly avoid numeric problems when either h or k are nearly zero.

Post-processing for Tinfour

The Tinfour AlphaCircle class performs an additional operation that is not strictly part of the alpha circle calculation.

In practice, one circle center always lies to the left of the line segment and one circle center always lies to its right. The Tinfour implementation uses this information as part of its logic for constructing the alpha shape. So, when computing the alpha circle centers, Tinfour ensures that the solutions are given in order so that the circle center to the left of the line segment is given first and the circle center to the right of the line segment is given second.