Managing a Virtual Raster
using a Tile-Cache Algorithm

by G.W. Lucas

Introduction

The Gridfour virtual raster management system provides a way to reduce the memory required for processing large and very large grid-based data sets. To do so, it divides the overall raster into smaller pieces (tiles) that can be swapped between memory and a large-capacity storage device such as a disk drive or Solid State Drive (SSD). When an application requires access to a particular part of the overall grid, that subsection is read into memory for processing, then discarded or written back to the supporting storage system when no longer needed. This approach is similar to the classic virtual memory technique. It represents a compromise between performance and available resources. Memory provides rapid access to data, but may be limited in size or needed for other uses. File-based storage is slower than memory, but provides much more capacity for storing data. The Gridfour virtual raster algorithm attempts to balance these two considerations.

Because reading and writing data to a high capacity storage device entails a substantial performance cost, a virtual raster system requires a mechanism for managing the exchange of data efficiently. The decision of when to load or discard a particular subsection of the grid should be based on the patterns-of-access for the calling application and should attempt to minimize the frequency with which data is transferred between memory and backing storage.

In Gridfour, the exchange of raster subsections (tiles) is managed using a tile-caching algorithm. Details of the Gridfour virtual raster technique are descibed below.

Concepts

Raster data

In computer programming, the term raster refers to any grid-based data set. There are many different kinds of raster products. The most common kind of raster is a digital image. A digital image is essentially a grid of data cells (pixels) each of which is assigned a numerical value, usually light or color intensity codes. But raster products also include mathematical objects such as matrices and geospatial grid products such as elevation data sets.

The tiling scheme

The basic idea of tiling a grid can be seen in the image below. In this case, a grid consisting of six rows and nine columns is divided into six 3-by-3 tiles.

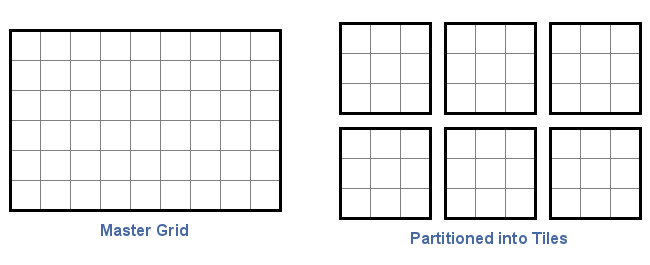
Figure 1 – A tiling scheme divides a master grid into uniformly sized sub-gribs.

The size of tiles is arbitrary. The Gridfour software libraries assume that all tiles must be of a uniform size, though other APIs may use non-uniform specifications. Applications are free to specify tile sizes according to their needs. In this case, a 2-by-9 tiling scheme would have worked just fine. In fact, a 4-by-5 tile size would also work, even though the tiles would not evenly divide the 6-by-9 master grid. The Gridfour APIs handle any extra cells internally and their management is transparent to the application.

The tile cache

When an entire grid is too large to be maintained in memory, a caching mechanism may implement a strategy for keeping the data that is most likely to be needed while deferring access to that part of the grid that is not immediately required. The Gridfour strategy is based on the assumption that when an application accesses one cell in a grid, there is a high probability that the next access will be to another cell in the proximity of the first. And, in many cases, the subsequent access of grid cells occur within the bounds of a single tile. This assumption is often applicable whether a raster product has a spatial basis (geophysical data) or not (image data, matrices).

Following that assumption, the tile cache is organized as a priority queue ordered by the time of most recent access. The most recently accessed tiles are placed at the head of the queue. The least recently accessed are placed toward its back. The queue is configured to hold an arbitrary maximum number of tiles based on the desired memory use for an application. Figure 1 below shows an example of a virtual raster consisting of a set of 3 rows and 3 columns of tiles. For purposes of illustration, the tile cache is configured to store a maximum of 3 tiles.

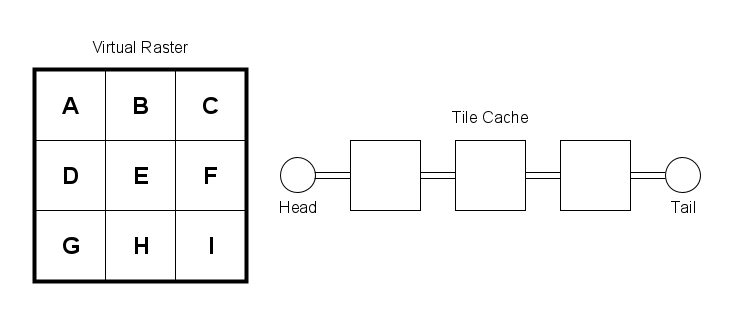
Figure 1 – A virtual raster and an empty tile cache.

The design of the cache algorithm is based on the assumption that memory is limited and that there is a significant performance cost in reading a tile from the associated high-capacity storage device. So the primary objective of the cache is to minimize redundant access to the backing storage device and to to provide a high likelihood that when a particular tile is needed, it will already be in memory. To address these goals the tile-cache algorithm applies the following steps:

  1. Identify the required tile based on the grid row and column indices to the desired data cell.
  2. Search the tile-cache queue to determine whether the target tile is already in the cache.
  3. If the tile is already in the cache:
    1. Move the tile to the first position in the queue.
    2. All other tiles are shifted to the right.
  4. If the tile is not in the cache:
    1. If the cache is full, discard the rightmost tile to make room for the target tile.
    2. Read the target tile from the backing storage device (i.e. a file) and insert at the head of the queue.
    3. All other tiles are shifted to the right.

The figure below illustrates the state of the tile cache over the course of three subsequent accesses to tiles A, B, and C. At the end of the sequence, the least-recently accessed tile, tile A, is shifted to the last (rightmost) position in the queue.

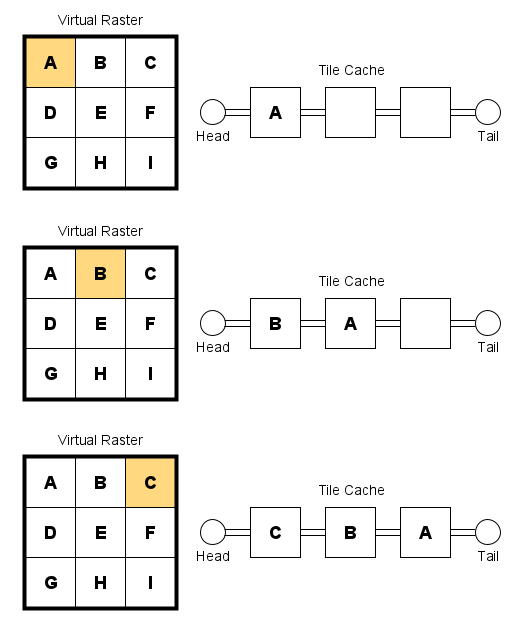
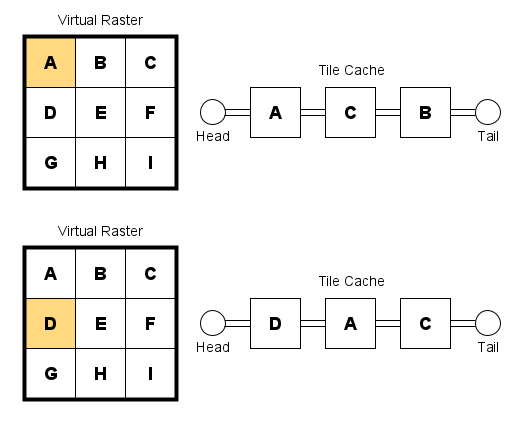
Figure 2– The cache, after inserting tiles A, B, and C.

If the application were to access tile A again, it would be moved to the head of the queue. Tiles C and B would be shifted to the right. Tile B, being the least-recently accessed tile, would be shifted to the last position in the queue. The figure below illustrates what happens when the application accesses an additional tile, D. Because tile B was the least-recently accessed tile, it would be discarded (or written to the backing store). The resulting cache would include tiles in the order D, A, and C, as shown in the figure below.

Figure 3 – The cache, after accessing tile A and inserting tile D.

Cache size and performance

An optimal selection of cache depends on two factors: the amount of memory that an application can allocate to the tile cache, and the anticipated pattern of access. Naturally, the tile cache provides an advantage when an application makes repeated accesses to tiles that are already loaded the cache.

The following use cases indicate different conditions under which the tile cache size may be configured to support the behavior of an application:

  1. The application accesses the grid in random or widely scattered positions: Most operations will require reading a new tile from the backing storage device. In such cases, the tile cache does not improve performance. A smaller cache size is preferred.
  2. The access sequence follows a multi-cell path across the grid: As an example, consider the case where a geospatial data set such as elevation and bathymetry grid is tied to the path of a vehicle (aircraft, ship, etc.). Access might alternate between adjacent tiles while gradually transitioning to different tiles as the vehicle moves across the region supported by the raster product. A medium size cache would perform well.
  3. An application scans the entire grid in row-major order: This use case is common in image processing or data-transcription operations. Each scan of a grid row will cross an entire row of tiles. So there is an advantage in making the tile cache large enough to hold a complete row of tiles. During processing, the set of tiles in the cache will be accessed multiple times. But, they will only be read from the backing storage device once. Redundant tile-read operations will be eliminated. Maintaining an entire row of tiles leads to a larger cache size, but the performance gain is significant.

Implementation

The Gridfour Software Project includes implementations of the tile cache in the Java and C programming languages. Both implementations are similar in their structure and approach. These notes will focus on the C implementation.

The tile index

The Gridfour API assigns integer codes to each tile in row-major order. The first tile in the first row of tiles is assigned the value zero. The tile to its right is assigned a value of one, and so forth. The tile index is used as primary key for identifying tiles in all of the data collections used to support the tile cache.

The tile queue implemented as a linked list

The tile queue is implemented using a doubly linked list. The tile cache maintains pointers to both the head and tail of the linked list. The doubly linked list structure provides a convenient way for the cache to move a tile to the head of queue when it is accessed by the application code. And because the API can access the linked list from its tail end, the list-based implementation allows the code to identify the least-recently used tile and discard it when the application needs to insert a new tile into the queue.

A hash table expedites searching the queue

When the application requires access to a tile, it could perform a sequential search of the tile queue. However, if the queue is configured to hold a large number of tiles, there could be a significant performance cost for the search. To expedite tile searches, the Gridfour API implements a hash table that maps a tile index to a node within the linked list. The table is implemented using an integer hash key which is computed directly from the tile index. For the Gridfour C implementation, a simple hash table is implemented in custom code.

Note that operations on the hash table and linked list structures must be coordinated. When a tile is added or removed from the list, it must also be added or removed from the hash table. On the other hand, moving a tile to the front of the list does not require a change to the hash table. Changing the order of tiles within a linked list is accomplished by modifying the list's link elements. But the tiles themselves are not modified and their location in memory does not change. Thus the corresponding tile-reference (or pointer) in the hash table does not have to be adjusted.

Practical examples

The Gridfour software project includes two implementations of the tile cache: one written in Java, and another written in C. The code for these implementations can be found on Github at the Gridfour Java repository and The Gridfour C repository.

To illustrate the role of a tile cache in software implementations, let's consider the ETOPO1 global elevation and ocean-depth (bathymetry) data set. ETOPO1 is organized in a grid based on geographic coordinates (latitude and longitude) with a raster cell spacing of one minute of arc (1/60th of a degree). The original source data was re-packaged in the GVRS format using a tile-size specification of 120 rows by 180 columns. This specification results in tiles that cover an area of 2 degrees of latitude (120 rows, one minute each) by 3 degrees of longitude (180 rows, one minute each). The tile size was selected through trial-and-error to provide a good balance between performance and effective data compression. The main parameters for ETOPO1 are given below:

	Data source:     ETOPO1_v1.0.4.gvrs   (uncompressed)
	Raster size:     10800 x 21600 for 233280000 grid cells
	Tile size:       120 x 180 for 10800 tiles
	Rows of tiles:   90
	Colums of tiles: 120
	File size:       455.9 MiB   (compressed  103.8 MiB)
	Data type:       2 byte integers

As described in the paragraph Cache-size and performance above, the Gridfour APIs permit an application to set a tile-cache size depending on the pattern of access. The Gridfour C implementation includes a function that prints a summary of the memory use for the standard tile-cache sizes:

	Tile cache size: Large,   4.9 MiB,    bytes per tile: 43200
	Options for standard cache sizes
	Size              Max Tiles      Max Memory (MiB)
	Small                     4                  0.2
	Medium                    9                  0.4
	Large                   120                  4.9
	Extra Large             240                  9.9

Both the C and Java source code distributions include example programs that demonstrate the use of their respective APIs. The C project includes two examples that illustrate pattern of access:

Example location queries using a small cache

The text below shows the output from the ExampleLocation program. Note that the locations are scattered throughout the raster product so that each accesses a separate tile.

	Name                              Lat         Lon       Elevation (m)
	Auckland, NZ                    -36.840,    174.740,         15.0
	Coachella, California, US        33.681,   -116.174,        -22.0
	Danbury, Connecticut, US         41.386,    -73.482,        154.0
	Dayton, Ohio, US                 39.784,    -84.110,        238.0
	Deming, New Mexico, US           32.268,   -107.757,       1324.0
	Denver, Colorado, US             39.739,   -104.985,       1602.0
	La Ciudad de México, MX          19.445,    -99.134,       2240.0
	La Paz, Bolivia                 -16.495,    -68.139,       3749.0
	Mauna Kea, US                    19.821,   -155.468,       4044.0
	McMurdo Station, Antarctica     -77.850,    166.692,         31.0
	Nantes, France                   47.218,     -1.553,         22.0
	Pontypridd, Wales                51.594,     -3.321,        129.0
	Québec, QC, Canada               46.812,    -71.205,         28.0
	Sioux Falls, South Dakota, US    43.568,    -96.725,        428.0
	Suzhou, CN                       31.335,    120.629,          5.0
	Zürich, CH                       47.380,      8.543,        435.0

Example row-major read performance for different cache sizes

The text below shows examples of the read performance using different sizes for the tile cache.

	Read Performance for file ETOPO1_v1.0.4.gvrs

	Cache-size Large  (120 tiles in cache)
		Test                     Time (sec)    Operations    Operations/sec
		Row Major Order            1.900        233280000   122778947.4
		Column Major Order         1.926        233280000   121121495.3

	Cache-size Medium (9 tiles in cache)
		Test                     Time (sec)    Operations    Operations/sec
		Row Major Order           19.437        233280000    12001852.1
		Column Major Order        25.621        233280000     9105031.0

From the descriptive parameters for ETOPO1, we see that there are 120 columns of tiles in the raster. So, in a row-major scan of the file, each row of the scan crosses 120 tiles. When the cache-size configuration is large, it can hold the entire row of tiles. For the scan of the first row, the API reads each tile and stores it in the cache. But every data query in the scan of the second row can be satisfied using a tile from the cache. No additional file access is required for the next several rows.

On the other hand, the medium-size cache is not large enough to hold an entire row of tiles. So most tiles will have dropped out of the cache by the time the scan of the second row begins. The medium-size configuration requires that tiles be read redundantly to satify the needs of the application. Thus, the access time for the medium cache is much larger than for the large cache.

The text above also shows access times for reading the file in column-major order. The results show that the tile-cache can be effective for patterns of access other than the row-major pattern. In the case of this particular GVRS file, the column-major access is somewhat slower than row major because the tiles themselves were collected in row-major order when the file was assembled. Accessing the tiles in column-major order requires more file-seek operations than the row-major order did. But this difference is an artifact of the way the data was collected, and will not be true in all cases.

Conclusion

The tile cache concept plays a key role in both the original Gridfour Java and newer Gridfour C software libraries. The source code for these projects provides examples of tile cache implementations. In both cases, the code includes small enhancements that were not described in this article because they are specific to the programming language used for the implementation. Developers wishing to create their own versions of a tile cache may find these elements worth review.