Introduction

The Tinfour open-source software project recently introduced a Java-based implementation of Ruppert’s Delaunay refinement method. To assist developers who wish to use the Tinfour implementation, or any other implementation of Delaunay refinement, these notes provide a brief introduction to the concepts and applications of this technique.

Concepts

The Delaunay triangulation is a technique for constructing an optimal triangular mesh from a set of unstructured (or “scattered”) points (see Lucas, 2017). It is often used for geophysical applications and in finite element analysis methods. One of the desirable qualities of the Delaunay is that it tends to produce “robust” triangles (i.e. it avoids constructing triangles with small angles). Unfortunately, there are many cases where the underlying geometry of the sample points or the presence of application-defined constraints results in the production of “skinny” triangles (i.e. flattened triangles with one or two very small angles). The presence of skinny triangles can lead to numeric issues in geometric calculations and may result in undesirable artifacts in graphics or physical modeling applications. Delaunay refinement techniques attempt to remedy this situation by introducing synthetic points (called “Steiner” points) at optimally selected locations to improve the quality of the Delaunay triangulation.

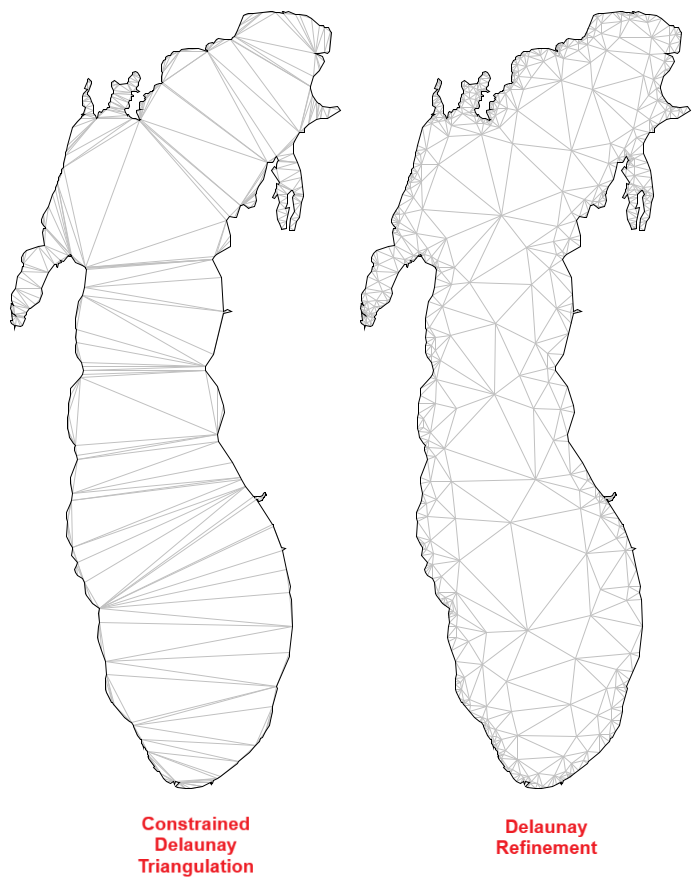
The figure below shows two views of Delaunay triangulations for Lake Michigan, one of the North American Great Lakes. The left panel shows the results of a constrained Delaunay triangulation constructed from a low-resolution digitized shoreline for the lake. The source data provides 616 points to describe about 1200 miles (1946 km) of shoreline. Because the shoreline represents a fixed, real-world object, the Delaunay triangulation is not allowed to modify the geometry of the edges that define the lake polygon. This constraint limits the ability of the Delaunay to optimize the triangles that it produces. So, even though the resulting mesh is “Delaunay conforming”, it is prone to the skinny triangles visible in the image.

To improve the overall quality of the mesh, the Delaunay refinement technique introduces Steiner points at optimally selected positions as shown in the panel to the right. In the figure, the vertices added in the open-water parts of the lake are Steiner points. In cases where a constrained edge is “encroached” by a vertex (i.e. the vertex lies too close to the edge), Ruppert’s technique implements logic to split the line at its midpoint. The split improves the quality of the local mesh by dividing the large obtuse angle of the adjacent triangle into smaller pieces. And because it occurs at the midpoint, this split operation does not alter the geometry of constrained line segment.

Delaunay refinement for Lake Michigan — Figure 1. — Constrained Delaunay triangulation for Lake Michigan before and after refinement (data source: U.S. National Ice Center, 2025; image source: Tinfour).

The Tinfour implementation of Ruppert’s Delaunay refinement method

There are a number of Delaunay refinement techniques. Tinfour software project includes a Java-based implementation of Ruppert’s method (Ruppert, 1995). Some characteristics of Ruppert’s method include:

Quality triangles: Ruppert’s method is designed to produce a mesh where all triangles have a minimum angle of at least some specified value. Ruppert showed that, except for triangles formed by intractable constrained angles, his algorithm would terminate successfully for minimum-angle specifications in the range 0 to about 20.7 degrees (Shewchuk, 2001, p. 5). Also, the resulting mesh is often better than the minimum angle. For the Lake Michigan example, we specified a minimum angle of 15 degrees. The average minimum angle across all non-constrained triangles is about 31°.
Good grading: The lengths of edges in the mesh (and the size of triangles) reflect the local feature size. In the Lake Michigan example, the triangles near the shore (where sample points are more densely spaced) are relatively small while those in the open-water range are much larger.
Potentially bounded domain: When a sample point set is bound by an enclosing polygon (a polygon constraint), Ruppert’s method will not generate new Steiner points outside the polygon. If the input is not bound by a polygon, Ruppert’s is free to insert Steiner points beyond the convex hull of an existing Delaunay triangulation.

Source data with intractable small angles

When a Steiner point is inserted into a Delaunay triangulation, it eliminates skinny triangles by deleting some edges and introducing others. But, by definition, constrained edges must be preserved and cannot be deleted. Thus constraints can prove challenging when two connected edges form an angle smaller than the minimum-angle specification for the refinement operation. For example, the Lake Michigan polygon has a number of small features representing the mouths of rivers, inlets, jetties, peninsulas, etc. These features commonly include pairs of connected line segments that form very small angles. Unfortunately, there are no satisfactory methods for applying Delaunay refinement in cases where these features need to be preserved. Ruppert and other authors have proposed techniques for minimizing their impact (for example, see the “Terminator” algorithm in Shewchuk, 2001). Most Delaunay refinement implementations include logic to handle problematic input sets.

Practical considerations

When using the Tinfour implementation, it may be useful to keep the following practical considerations in mind.

Varied input: Input sources may include a combination of line and polygon constraints, as well as conventional vertices. However, the input Delaunay triangulation (i.e. an instance of one of the incremental TIN classes) must be Delaunay compliant. This setting is specified by the restoreConformity argument for the IIncrementalTin.addConstraints() method.
Minimum angle specification: Minimum angles larger than 20.7 degrees are permitted, but may result in longer run times. In the Lake Michigan example, a minimum angle specification of 20.7 degrees resulted in an average minimum angle of 35.7 degrees with a program run time of less than 1 second on a commodity laptop computer. However, a specification of 30 degrees resulted in an average minimum angle of 46.4 degrees, but required a run time of over 6 seconds.
Minimum triangle area specification: The implementation attempts to avoid problematic conditions by not attempting to refine triangles smaller than a specified size.

Additional processing options are described in the class documentation.

Conclusion

These notes provide a very brief introduction to the ideas of Delaunay refinement. While they should be enough to get you started using Tinfour’s Java-based Delaunay refinement classes, there are many opportunities for further reading if you are interested. The topic of Delaunay refinement has been extensively studied and discussed in the published literature. In particular, we recommend looking at the work of Jonathan Shewchuk (for example, Shewchuk, 2001). Mr. Shewchuk is an accomplished writer whose work presents a rare combination of readability and a deep mathematical knowledge of the Delaunay triangulation and refinement algorithms.

Future work

The Tinfour free open-source software project is continuing work on its Java-based Delaunay refinement classes. We are currently looking into improved metrics and performance with special attention to scalability issues.

References

Delaunay, Boris (1934). "Sur la sphère vide", _Otdelenie Matematicheskikh i Estestvennykh Nauk 7_, p. 793–800

Lucas, G. (2017). An introduction to the Delaunay triangulation. Tinfour Software Project (Github). Accessed Nov. 2025 from https://gwlucastrig.github.io/TinfourDocs/DelaunayIntro/.

Ruppert, J. (1995). A Delaunay refinement algorithm for quality 2-dimensional mesh generation. Journal of Algorithms, Volume 18, Issue 3, pg. 548-585. Downloaded Nov. 2025 from https://www.cis.upenn.edu/~cis6100/ruppert.pdf.

Shewchuk, J. (2001). Delaunay refinement algorithms for triangular mesh generation. Department of Electical Engineering and Computer Science, University of California, Berkeley. Accessed Nov. 2025 from https://people.eecs.berkeley.edu/~jrs/papers/2dj.pdf.

U.S. National Ice Center (USNIC). (2025). Great Lakes data support files. File: GL20250515_lam.shp. Downloaded Oct. 2025 from https://usicecenter.gov/Products/GreatLakesData